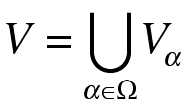
More Precisely
The Math You Need to do Philosophy
Books
More Precisely
Chapter Abstracts
More Precisely is a mathematics book for philosophers. It introduces the formal tools used in philosophy, and illustrates the applications of those tools with examples from both classical and contemporary philosophy.
These are the chapter abstracts for the Second Edition, expected to appear in late 2017.
Chapter 1: Sets
We begin with the language of sets and the basic ideas of set theory. Our discussion is by way of examples rather than by way of axioms. The topics discussed are: set-builder notation; the membership relation; identity for sets; the subset relation; the empty set; unit sets; sets of individuals; pure sets. We talk about various operations on sets, including unions, intersections, differences, and the power set operation. We introduce the notion of sets as selections, sets of sets, and the iterative hierarchy of sets. We talk briefly about how various mathematical objects can be built out of sets. The chapter ends by introducing ordered pairs, n-tuples, and Cartesian products.
Chapter 2: Relations
From basic set theory, we move to relations and functions. It opens with the basics: relations are sets of ordered n-tuples; relations have properties like reflexivity, symmetry, and transitivity. After presenting the basics, the chapter talks about order relations, then discusses closures, ancestrals, equivalence relations and equivalence classes. We use the classical memory theory of personal identity to illustrate equivalence relations. Starting with a basic memory relation, we take the symmetric, then transitive, then reflexive closures to make an equivalence relation. We then discuss the problems introduced by the notion of personal fission. We show how taking the symmetric then transitive closure is distinct from taking the transitive then symmetric closure. Functions are used everywhere in philosophy. So we spend a good deal of time discussing functions. We talk about the features and types of functions. We briefly illustrate their use in philosophy of language and science. Since many branches of philosophy make use of isomorphisms, we introduce and illustrate the notion of isomorphism.
Chapter 3: Machines
Machines play many roles in philosophy, both in the philosophy of mind and the philosophy of physics. This chapter introduces machines and cellular automata. A machine is a formal structure used to describe some lawful pattern of activity. Machines are often used in philosophy of mind - many philosophers model minds as machines. Machines are sometimes used in metaphysics - simple universes can be modeled as networks of interacting machines. You can use these models to study space, time, and causality. We start by introducing finite state machines. We discuss programs and dispositions. Mechanical universes are networks of machines. We illustrate the concept of a mechanical universe with the game of life. The chapter also contains a brief introduction to Turing machines.
Chapter 4: Semantics
The philosophy of language makes extensive use of set theory. Sets, relations, and functions are extensively used in formal semantic theories. So this chapter can be thought of as an opportunity to apply the set-theory defined in the first two chapters. We develop a simple version of extensional semantics. We define a reference function that maps words onto their referents. The referent of a name is a thing; the referents of predicates are sets of things or sets of n-tuples of things. The next topic is truth-conditions of sentences. These truth-conditions make heavy use of the membership relation. We look at basic possible worlds semantics. Possible worlds semantics is illustrated with a simple model with several worlds. Truth-conditions are supplied for many kinds of sentences. We show how properties and propositions can be analyzed in terms of sets. Finally, we develop possible worlds semantics using counterpart theory. We discuss de re and de dicto modalities. Again, we use a simple model with many worlds to illustrate our discussion, and we provide truth-conditions for many kinds of sentences.
Chapter 5: Probability
This chapter introduces basic probability theory. Probability theory is used in epistemology and philosophy of science (e.g. Bayesian epistemology, Bayesian confirmation theory). The topics here include experiments and sample spaces; simple probabilities; combined probabilities; probability distributions; and conditional probabilities. Many examples are provided to illustrate these concepts. The philosophical fun begins with Bayes Theorem. After our discussion of Bayes Theorem, we consider various philosophical applications. We talk about degrees of belief and subjective probability functions. We discuss Bayesian confirmation theory. All our discussions contain many examples.
Chapter 6: Information Theory
Familiarity with the concepts of information theory is useful in many branches of philosophy, such as epistemology, aesthetics, and the philosophy of mind. This chapter begins with a discussion of messages, codes, and channels. It describes the ways that messages can be coded. It develops the idea of compression using Huffman codes. It then moves into an extensive discussion of the concept of entropy, including joint entropy. From entropy, it moves to mutual information. Mutual information is useful in the analysis of mental representation. The chapter ends with a discussion of the analysis of consciousness using integrated information theory.
Chapter 7: Decisions and Games
Here we discuss some of the math used in decision theory and game theory. These theories are relevant in ethics. This chapter opens with some of the math used in simple versions of act utilitarianism. We briefly talk about expected utility and rational choice - thus showing again how probability is applied in philosophy. The chapter then moves on to game theory. It introduces payoff matrices using static games like rock-paper-scissors. It then turns to the prisoner's dilemma, a game with many interesting philosophical issues. It discusses dominant strategies and Nash equilibria, using many other examples of games, such as the Stag Hunt. It discusses the iterated prisoner's dilemma, and the iterated spatialized prisoner's dilemma, and then turns to public goods games. These games are used to introduce the mathematical concepts behind the evolution of cooperation. The evolution of cooperation is relevant in ethics and political philosophy.
Chapter 8: Infinity
The topic of infinity comes up in many philosophical discussions. Is the mind finitely or infinitely complex? Can infinitely many tasks be done in finite time? What does it mean to say that God is infinite? We open with a discussion of recursively defined sequences. We show how to add limit clauses to such definitions. We talk about acceleration. We show how recursively define sequences and limits have been used in philosophy. Our examples include Zeno's racetrack, Royce's definition of the divine mind as a self-representative system, and an infinitary version of the degrees of perfection argument for God. The chapter thus moves to the notion of countable infinity. We define infinity and illustrate the definition. Of course, we talk about the Hilbert Hotel. We discuss supertasks, including infinitary computations and the notion of accelerating Turing machines.
Chapter 9: Bigger Infinities
There exists an endless progression of bigger and bigger infinities. We discuss the difference between ordinal and cardinal numbers. The chapter gives an extensive discussion of Cantor's Diagonal Argument and Power Set Argument. These are two of the most brilliant arguments ever produced. As examples of pure reasoning, they are highly philosophically valuable. We introduce the beth numbers, the alephs, and the continuum problem. We turn at last to the transfinite ordinal number line and to the notion of transfinite recursion. The chapter concludes with an application of transfinite recursion in philosophy of religion.